MAT.5.3.7. Matematiksel araç ve teknoloji yardımıyla düzlemde iki noktada kesişen çember çiftinin merkezleri ve kesişim noktalarından biri ile inşa edilen üçgenlerin kenar özelliklerine yönelik muhakeme yapabilme.
a) İki noktada kesişen çember çiftinin merkezleri ve kesişim noktalarından biri ile inşa edilebilecek üçgenlerin kenar özelliklerine yönelik varsayımlarda bulunur.
b) Örnek çizimler üzerinden, kesişen iki çemberin merkezleri ve kesişim noktalarından biri ile inşa edilen çeşitkenar, ikizkenar ve eşkenar üçgenleri belirler.
c) Belirlediği üçgenlerin özelliklerini varsayımları ile karşılaştırır.
ç) Varsayımlarını, inşa ettiği üçgenler ile karşılaştırarak doğrulayabileceği önermeler şeklinde ifade eder.
d) Sunduğu önermelerin katkısını değerlendirir.
e) Çemberin özelliklerini kullanarak önermelerini doğrulamaya yönelik matematiksel gerekçeler sunar.
f) Çemberin özelliklerinin benzer inşa süreçlerindeki rolünü değerlendirir.
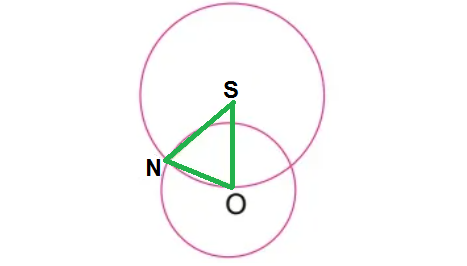



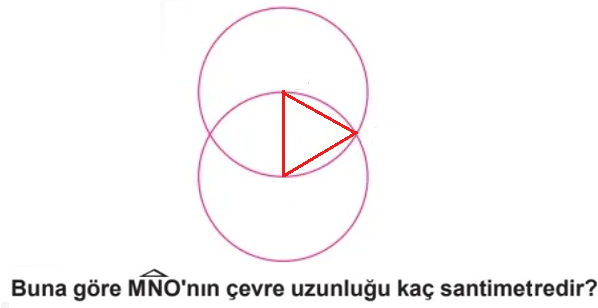
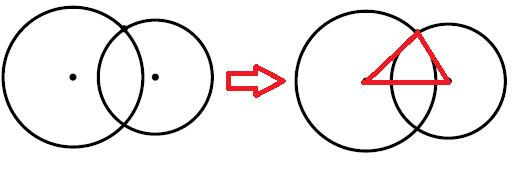
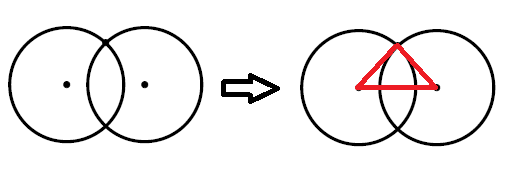
Aşağıdaki ifadelerden hangisi yanlıştır?





MAT.5.3.7. Matematiksel araç ve teknoloji yardımıyla düzlemde iki noktada kesişen çember çiftinin merkezleri ve kesişim noktalarından biri ile inşa edilen üçgenlerin kenar özelliklerine yönelik muhakeme yapabilme
a) İki noktada kesişen çember çiftinin merkezleri ve kesişim noktalarından biri ile inşa edilebilecek üçgenlerin kenar özelliklerine yönelik varsayımlarda bulunur.
b) Örnek çizimler üzerinden, kesişen iki çemberin merkezleri ve kesişim noktalarından biri ile inşa edilen çeşitkenar, ikizkenar ve eşkenar üçgenleri belirler.
c) Belirlediği üçgenlerin özelliklerini varsayımları ile karşılaştırır.
ç) Varsayımlarını, inşa ettiği üçgenler ile karşılaştırarak doğrulayabileceği
önermeler şeklinde ifade eder.
d) Sunduğu önermelerin katkısını değerlendirir.
e) Çemberin özelliklerini kullanarak önermelerini doğrulamaya yönelik matematiksel gerekçeler sunar.
f) Çemberin özelliklerinin benzer inşa süreçlerindeki rolünü değerlendirir.